椭圆曲线加密（ECC，Elliptic Curve Cryptography）是一种基于椭圆曲线数学的公钥加密技术，以其高安全性和高效性著称。以下从基础概念到实际应用进行详细解析：

ECC的核心优势

  1. 短密钥高安全：相比RSA，ECC的密钥长度更短。例如，256位ECC密钥的安全强度相当于3072位RSA密钥
  2. 高效计算：ECC的加密、解密和签名生成速度更快，适合资源受限环境（如物联网设备、移动端）。
  3. 带宽节省：短密钥减少数据传输量，提升网络效率。

椭圆曲线的数学基础

  1. 椭圆曲线方程
  • 标准形式：y2 = x 3 + ax + b(其中4a3 + 27 b2 !=0，避免奇点 )
  • 图形特性：关于x轴对称，光滑无自交点。
  1. 椭圆曲线上的点加法

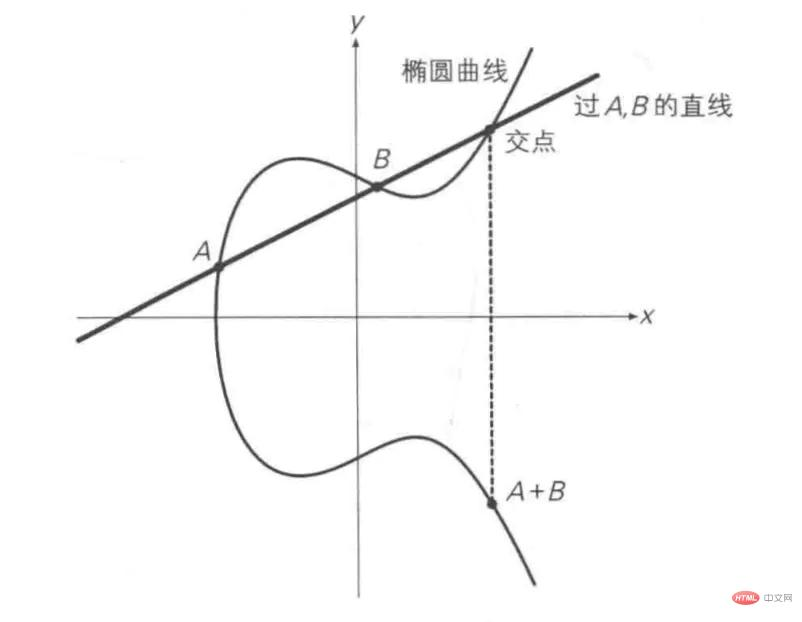
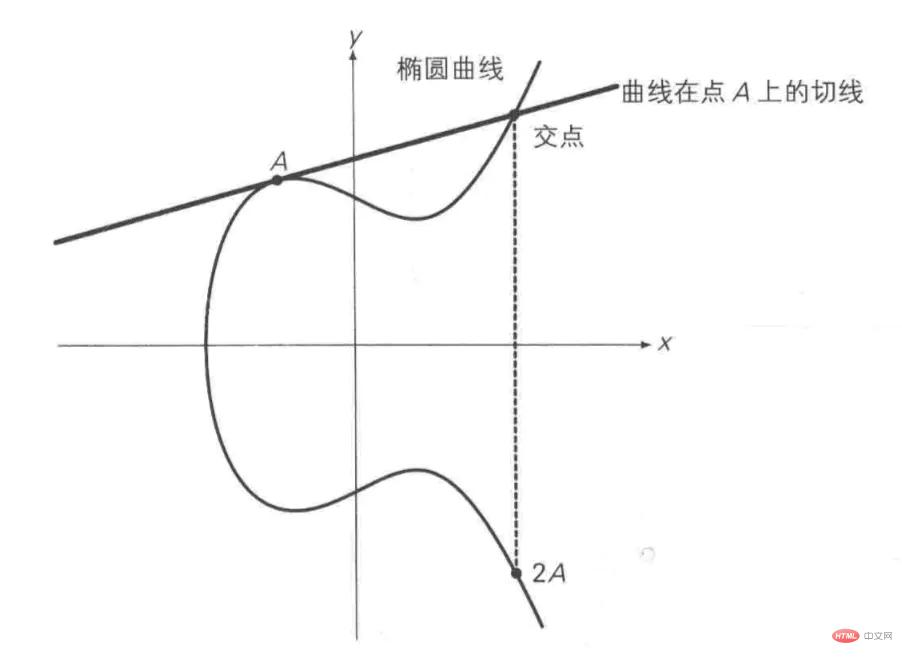
几何解释：
点加（P ≠ Q）：画直线通过P和Q，交曲线于第三点R，取对称点-R即为P+Q。
点倍（P = Q）：取P点切线，交曲线于R，对称点-R即为2P。

例1 例2
  1. 群结构与标量乘法
  • 加法群：椭圆曲线上的点及无穷远点构成阿贝尔群。
  • 标量乘法：核心操作 kP = P + P + …… + P(k次)，私钥为整数k，公钥为点kG（G为公开基点）。

ECDLP难题：已知kG和G，求k在计算上不可行（无已知亚指数时间算法），保障ECC安全

ECC加密

  • 公私钥生成

    1. Alice选择椭圆曲线E，在曲线上选择一点P作为生成元，并求P的阶为n，要求P为质数。
    2. Alice选定⼀个⼤数k作为私钥 (k < n)，生成公钥Q = kP。
    3. Alice将公钥组E、Q、P发送给Bob。

  • 加密

    1. Bob收到信息后，将明文编码为曲线上一点M，并选择一个随机数r (r < n)。
    2. Bob将消息M生成密文C： 密文是一个点对，即C=（rP，M+rQ）
    3. Bob密文发送给Alice

  • 解密

    1. Alice收到密文后，计算 M + rQ - k * （rP） = M + r（kp） - k（rp） = M，以获得明文M

ECC椭圆曲线加密算法相比RSA的优势分析

在当今的数字安全领域，非对称加密算法扮演着至关重要的角色。RSA作为传统加密算法的代表，与新兴的ECC（Elliptic Curve Cryptography）椭圆曲线加密算法相比，正逐渐显露出其局限性。

特性 ECC RSA
密钥长度 256位（等效RSA 3072位） 3072位
计算效率 快（适合移动设备） 慢（大数运算复杂）
内存/带宽占用 低 高
安全基础 椭圆曲线离散对数（ECDLP） 大数分解（IFP）

实际应用场景

  1. 移动设备：Apple iMessage使用ECC-256进行端到端加密
  2. 数字证书：Let’s Encrypt支持ECC证书（比RSA证书小50%）
  3. 区块链：比特币使用secp256k1椭圆曲线
  4. TLS 1.3：优先支持ECC算法套件

兼容性现状

虽然ECC具有诸多优势，但实际部署时需注意：

  • 旧系统兼容性（如Windows XP不支持ECC）
  • 需要正确选择曲线参数（推荐使用NIST标准曲线）
  • 证书链需要完整的ECC支持

结论

ECC椭圆曲线加密算法凭借其：
✅ 更短的密钥长度
✅ 更高的计算效率
✅ 更强的单位比特安全性
✅ 更低的资源消耗

正在逐步取代RSA成为新一代非对称加密标准。对于新系统开发，建议优先考虑ECC算法，而在需要兼容旧系统的场景中，可采用ECC+RSA的混合加密方案。